コンピュータ概要

データ表現

少数の表現(2進数

少数の表現には固定少数点数と浮動小数点数という2種類があります。

固定小数点数

以下の2進数が固定小数点数である場合の計算方法を説明します。

1010(2進数)
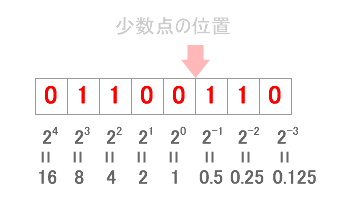
この数値の先頭ビットの前に小数点があるとすると・・・・

↓

1×2^-1 + 0×2^-2 + 1×2^-3 + 0×2^-4 = 0.5 + 0.125
= 0.625(10進数)

というように2進数の左の桁から2^-1,2^-2、2^-3と重みを付けて計算します。

この表現には弱点があり、0.6など5で割り切れない数値の場合

0.6（10進数）

≒1×2^-1 + 0×2^-2 + 0×2^-3 + 1×2^-4 + 1×2^-5 ・・・・・・

= 0.5+ 0.0625+0.03125 + ・・・・・・

= 10011・・・・・(2進数)

というように、いくら桁を用意しても（無限にビット用意しても）0.6には近づきますが、正確に0.6という数値を表現することはできません。結局は「8ビットまでは使う」など、ある程度の桁数に決めて、足りない分あきらめて切り捨てるということになります。